Setelah kita mempelajari konsep-konsep dasar gaya gesek maka disini kita sudah siap untuk merambah ke level selanjutnya. Ya, disini kita akan belajar melakukan proses analisis/perhitungan terhadap gaya gesek pada bidang datar dan bidang miring.
Selesai! Sampai di sini nilai gaya gesek sudah diketahui. Namun jika kalian dituntut untuk mengetahui berapa besar percepatan sistem (pada arah horizontal) maka solusinya adalah dengan mengaplikasikan hukum Newton 2.
* Nilai f negatif karena berlawanan dengan arah gerak
* F sin θ dan w bernilai negatif karena arahnya berlawanan dengan arah gaya normal.
Sehingga hasil akhirnya adalah,
a = {F ( cos θ + µsin θ ) - µmg} : m
Analisis Gaya Gesek pada Bidang Miring
∑F = 0
N - w sin θ = 0
N = w sin θ
Baru setelah itu masukan nilai N ke rumus gaya gesek:
f = µN
f = µ . w cos θ
Sedangkan untuk mencari percepatan sistem pada arah sumbu x (horizontal) bisa diketahui dengan mengaplikasikan hukum 2 Newton berikut:
∑F =ma
w sin θ - f = ma
w sin θ - µ w cos θ = ma
mg sin θ - µ mg cos θ = ma
sehingga hasil akhirnya,
a = g (sin θ - µ cos θ)
<<Kembali ke materi dinamika gerak lurus
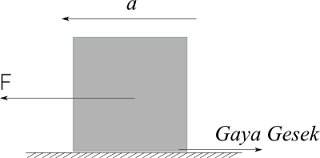
Analisis gaya gesek pada bidang datar I
Perhatikan gambar berikut!
Terlihat ada sebuah balok dengan berat w didorong dengan arah horizontal sebesar F. Untuk menghitung berapa besar gaya geseknya (f) tentu yang pertama kali kita lakukan adalah mencari gaya normalnya terlebih dahulu.
Sebagaimana yang dijelaskan pada ulasan pembahasan tentang gaya normal didapatkan:
∑F = 0
N - w = 0
N = w
Nah sekarang kita sudah mengetahui bahwa besar gaya normal pada sistem di atas adalah w. Sekarang saatnya memasukan nilai gaya normal tersebut ke rumus gaya gesek:
f = µ . N = µmg
Selesai! Sampai di sini nilai gaya gesek sudah diketahui. Namun jika kalian dituntut untuk mengetahui berapa besar percepatan sistem (pada arah horizontal) maka solusinya adalah dengan mengaplikasikan hukum Newton 2.
Perhatikan gaya-gaya yang terdapat pada arah horizontal. Kita menemukan ada yang namanya gaya F dan juga gaya gesek f.
Sehingga,

Sehingga,
∑F = ma
F - f = ma
* Nilai f negatif karena berlawanan dengan arah gerak
Sehingga berdasarkan persamaan diatas akhirnya diperoleh persamaan besar percepatan:
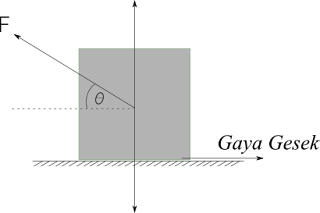
Analisis gaya gesek pada bidang datar II
Sistem di atas adalah analisis gaya gesek dengan keadaan dimana gaya luar tidak membentuk sudut θ
alias 0. Terus bagaimana jika sistemnya seperti gambar berikut?
Sama seperti cara diatas, untuk menghitung berapa besar gaya gesek, pertama kita harus mencari tahu dulu nilai gaya normalnya. Dimana gaya normal bisa diketahui dengan memperhatikan gaya-gaya yang terdapat pada arah vertikal.
Disana kita mendapatkan w, N dan F sin θ. Ketiga jenis gaya tersebut adalah komponen gaya pada arah vertikal. Dengan mengaplikasikan hukum 1 Newton didapat:
N + F sin θ
= w
N = w - F sin θ
N = mg - F sin θ
* F sin θ dan w bernilai negatif karena arahnya berlawanan dengan arah gaya normal.
Substitusikan persamaan tersebut ke rumus gaya gesek:
f = µN = µ(mg - F sin θ)
Sampai disini besar gaya gesek sudah diketahui. Selanjutnya jika kalian ingin mencari besar percepatan sistem pada arah horizontal bisa diketahui dengan memperguanakan hukum 2 Newton berikut.
∑F = ma
F cos θ
- f = ma
F cos θ
- µ(mg - F sin θ) = ma
F cos θ
- µmg + µF sin θ = ma
F ( cos θ
+ µsin θ
) - µmg = ma
a = {F ( cos θ + µsin θ ) - µmg} : m
Analisis Gaya Gesek pada Bidang Miring
Perhatikan gambar berikut!
Gambar diatas menginformasikan kepada kita bahwa ada sebuah benda dengan berat w tengah disimpan di permukaan bidang miring yang membetuk sudut θ. Untuk menentukan berapa besar gaya geseknya kita cari dulu besar gaya normalnya dengan persamaan:
∑F = 0
N - w sin θ = 0
N = w sin θ
Baru setelah itu masukan nilai N ke rumus gaya gesek:
f = µN
f = µ . w cos θ
Sedangkan untuk mencari percepatan sistem pada arah sumbu x (horizontal) bisa diketahui dengan mengaplikasikan hukum 2 Newton berikut:
∑F =ma
w sin θ - f = ma
w sin θ - µ w cos θ = ma
mg sin θ - µ mg cos θ = ma
sehingga hasil akhirnya,
a = g (sin θ - µ cos θ)
<<Kembali ke materi dinamika gerak lurus