Hi semuanya! Pada halaman ini kalian akan kami ajak untuk mempelajari sekaligus mengkaji tentang besaran vektor dan besaran skalar.
Apa itu besaran vektor? dan apa itu besaran skalar?
Berikut penjelasannya,
Pengertian Besaran Vektor dan Besaran Skalar
Besaran vektor adalah besaran yang mempunyai nilai sekaligus arah, sedangkan besaran skalar hanya memiliki nilai saja.
Maksudnya bagaimana?
Besaran vektor dikatakan memiliki arah sekaligus nilai karena jenis besaran ini dalam pemaparannya nanti akan diperlihatkan arah geraknya dengan nilai tertentu. Contohnya adalah kecepatan. Sebuah mobil dengan kecepatan 10 m/s tengah bergerak ke arah timur. Lihat ada nilai dan disebutkan juga arahnya!
Jika tidak disebutkan arahnya pun kecepatan akan selalu memiliki nilai dan arah, contohnya saat kita melihat mobil dengan kecepatan sekian. . . sekian, apakah kita bisa melihat arahnya kemana? Tetap bisa bukan.
Nah inilah kenapa kecepatan disebut dengan besaran vektor. Contoh lain dari besaran vektor adalah perpindahan, percepatan, gaya, berat, momentum, impuls, momen gaya dan lain-lain.
Nah jika besaran skalar contohnya seperti apa? Hmm. . . Saya ambil salah satu contoh besaran skalarnya adalah volume. Lho kok bisa?
Saya tanya kembali, apakah volume mampu menghasilkan arah seperti kecepatan yang saya sebutkan tadi? Tidak bukan. Oleh sebab itulah kenapa volume masuk ke ranah besaran skalar.
Contoh lain dari besaran skalar adalah semua besaran pokok, jarak, energi, kelajuan, usaha, potensial listrik dan masih banyak lagi.
Menentukan Resultan Vektor (R)
Maksud dari resultan vektor apa si? Resultan vektor disini maksudnya adalah memadukan atau menjumlahkan nilai-nilai sebuah vektor.
Dalam mencari resultan suatu vektor terdapat beberapa cara yang bisa dipergunakan. Tergantung kita mau mempergunakan yang mana. Ada yang disebut dengan metode Poligon, metode jajarg genjang dan analisis vektor.
1. Menjumlahkan Vektor dengan Metode Poligon
Pada dasarnya dalam mempergunakan metode poligon ini kita disuruh untuk menyambung serta menyusun beberapa vektor sampai terkondisikan titik pangkal terhubung ke titik ujung.
Bingung? Ini contohnya.

Dalam mencari resultan suatu vektor terdapat beberapa cara yang bisa dipergunakan. Tergantung kita mau mempergunakan yang mana. Ada yang disebut dengan metode Poligon, metode jajarg genjang dan analisis vektor.
1. Menjumlahkan Vektor dengan Metode Poligon
Pada dasarnya dalam mempergunakan metode poligon ini kita disuruh untuk menyambung serta menyusun beberapa vektor sampai terkondisikan titik pangkal terhubung ke titik ujung.
Bingung? Ini contohnya.

Nah perhatikan gambar diatas, antar satu vektor dengan vektor yang lainnya saling terhubung. Dimana setiap ujung vektor terhubung ke pangkal vektor yang lainnya. Jika sudah dihasilkan seperti keadaan diatas, nilai resultan bisa diketahui dengan cara menjumlahkannya.
R = a + b + c
2. Menjumlahkan vektor dengan metode jajargenjang
Bagi kalian yang ingin menghitung berapa besar resultan vektor dengan metode jajargenjang, bisa ikuti langkah-langkahnya berikut:
a. Gambarkan 2 buah vektor dengan satu titik tangkap yang sama
b. Buat bayangan untuk setiap vektor
c. Buat garis baru dari titik pertemuan vektor dengan titik tangkap bayangan
Untuk ilustrasinya bisa dilihat pada gambar dibawah:

R = a + b + c
2. Menjumlahkan vektor dengan metode jajargenjang
Bagi kalian yang ingin menghitung berapa besar resultan vektor dengan metode jajargenjang, bisa ikuti langkah-langkahnya berikut:
a. Gambarkan 2 buah vektor dengan satu titik tangkap yang sama
b. Buat bayangan untuk setiap vektor
c. Buat garis baru dari titik pertemuan vektor dengan titik tangkap bayangan
Untuk ilustrasinya bisa dilihat pada gambar dibawah:

Berdasarkan gambar diatas, kita melihat sebuah jajargenjang dengan garis merah membentang ditengahnya. Garis tengah inilah yang disebut dengan resultan vektor. Nilai dari resultan vektor bisa didapat dengan mempergunakan rumus:
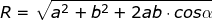
dimana α adalah sudut yang dibentuk oleh kedua vektor
3. Analisis Vektor
Ketika didapati sebuah vektor dengan nilai ternetu, kita bisa menguraikannya ke dalam komponen-komponen sumbu X dan komponen sumbu Y.

Nilai-nilai untuk setiap komponen tersebut bisa dicari dengan:
Fx = F cos α
Fy = F sin α
dimana α adalah sudut yang dibentuk oleh kedua vektor
3. Analisis Vektor
Ketika didapati sebuah vektor dengan nilai ternetu, kita bisa menguraikannya ke dalam komponen-komponen sumbu X dan komponen sumbu Y.

Nilai-nilai untuk setiap komponen tersebut bisa dicari dengan:
Fx = F cos α
Fy = F sin α
Subab Materi Besaran dan Satuan
Silahkan pelajari subab dari materi besaran dan turunan di bawah secara berurutan:
- Besaran Pokok dan Besaran Turunan
- Pembahasan Dimens
- Awal Satuan dan Konversi
- Pembahasan Besaran Vektor dan Skalar
- Pengukuran dalam fisika





